© Котлярова Елена
Введение
Толпа является одной из составляющих общества. Моделирование поведения толпы имеет практическое значение при проектировании сложных архитектурных объектов, рассчитанных на большое количество людей, таких, как стадионы или публичные лектории.
Можно выделить несколько черт свойственных поведению людей в толпе:
- Формирование потоков движения в толпах, бывших стационарными до этого
- Формирование полос движения, когда пешеходы двигаются в разных направлениях
- Формирование кругового движения при пересечении встречных потоков
Также в толпах наблюдаются эффекты, связанные со скоростью и силой движения, с давлением толпы на пешехода. Люди в толпе не могут попасть в двери или пройти мимо друг друга при большой скорости движения. Сила толпы может сбивать пешеходов от намеченной траектории движения, ставя их под риск получения травмы.
Исходя из сказанного выше, в моделях поведения толпы необходимо учитывать не только потоки движения, образуемые толпой, но и влияние давления толпы и наличия в ней раненных на скорость и направление потоков. Так как модели, учитывающие давление, которое оказывает каждый индивид на своих соседей содержат много сложной математики и качественно не меняют выводов, авторы статьи предлагают модель, в которой влияние и сила толпы распределяется по группам и передается от группы к группе.
Базовая модель Кирчнера Kierchner
Модельное пространство представляет собой сетку с квадратными ячейками. Каждая ячейка представляет собой информационное множество, содержащее информацию двух типов:
- Тип 1 – статическое поле с информацией о расстоянии до ближайшего выхода;
- Тип 2 – динамическое поле определяет движение агента в потоке, получив информацию второго типа, агент может двигаться рядом с другими агентами, не мешая им, хотя точно не знает их стратегию движения.
Агенту доступны информационные множества, расположенные на его клетке и на клетках, соседних со сторонами клетки, на которой он стоит.
Ходы игроков
1) Для каждой клетки рассчитывается выигрыш:
– выигрыш на клетке i
– оценка информации типа 2 в клетке i
– оценка информации типа 1 в клетке i
– масштабирующие параметры, отражающие, соответственно, степень знания игрока о движениях других игроков и расположении выходов
2) Во время хода игрок может либо остаться в своей клетке, либо переместиться в 4 смежные клетки, находящиеся с четырех сторон от его ячейки. Чтобы определить, в какую клетку перейти, агент сравнивает вероятности перехода в разные клетки, задаваемые как
– вероятность перехода из ячейки i в ячейку j
– набор возможных клеток для перехода
3) Все игроки одновременно ходят и увеличивают 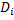своей начальной клетки на единицу, если перемещаются на другую клетку. Если агент остался в своей ячейке, что 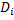не увеличивается.
своей начальной клетки на единицу, если перемещаются на другую клетку. Если агент остался в своей ячейке, что не увеличивается.4) Если больше одного игрока хотят встать на одну и ту же клетку, то выбирается случайный игрок, который переходит на эту клетку, все остальные остаются на месте.
5) Дальше величина 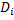«распадается и разлагается». Распад происходит путем переноса части на соседние клетки, другая часть разлагается и исчезает.
«распадается и разлагается». Распад происходит путем переноса части 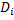на соседние клетки, другая часть 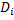разлагается и исчезает.6) Агенты, попавшие на клетку «выход», выходят из модели.
Модификация модели для отражения сил толпы
Пять особенностей применения силы в толпе:
1) Люди в толпе не толкают друг друга случайно. Они толкаются если а) хотят пройти в направлении толчка, б) хотят остаться на месте;
2) В толпе существуют толчковые волны, которые распространяют толчки по толпе в определенном направлении за определенное время;
3) Силы в толпе имеют направление, поэтому должны моделироваться не числами, а векторами;
4) С точки зрения составителя модели применение силы в толпе может повлечь два последствия: а) если толчок очень сильный и грубый, он может ранить человека, раненный человек становится препятствием для прохода других людей, б) если толчок не настолько силен, чтобы ранить, но все равно удар силен, то жертва толчка вынуждена поменять направление своего движения в сторону, куда ее толкнули, даже если агент не желал туда идти;
5) Сила давления в толпе возрастает с возрастанием количества толкающихся людей, поэтому чем плотнее расположены толкающиеся люди, тем вероятнее возникновение раненных людей.
В модели сила представлена в виде добавления к информационному множеству ячейки информации третьего типа. Третий тип информации содержит знание о том, насколько сильно давление на человека, стоящего в клетке, и какого его направление (информация задана в виде вектора).
Агенты применяют силу в двух случаях:
1) Агент хочет переместиться в уже занятую клетку, тогда он толкнет агента, находящегося в этой клетке, за ее пределами. Иными словами добавит к информационному множеству желаемой клетки вектор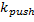 
2) Для удержания своего места в толпе агент применяет силу сопротивления к агентам, стоящим в соседних клетках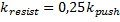 
Агенты следуют правилам движения модели Кричнера со следующим исключением: если давление, оказываемое на агента, превышает силу, которую он может противопоставить этому давлению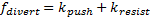 
, тогда агент меняет направление своего движения, повинуясь толпе.
, тогда агент меняет направление своего движения, повинуясь толпе.Правило распространения силы: давление перемещается от клетки к клетке по вектору приложения силы, таким образом, давление каждый раз перемещается среди толпы. Давление не может перемещаться сквозь пустые ячейки, если давление проходит через пустую ячейку, его сила становится равной нулю. Стены и препятствия также абсорбируют давление.
Ранения: агенты травмируются, если давление на них превышает допустимый порог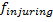 
, задаваемый как входной параметр модели. Для этой цели используется скалярная сумма сил вместо векторной. Как только агент получает травму, клетка, на которой он находится, становится препятствием для всех остальных.
, задаваемый как входной параметр модели. Для этой цели используется скалярная сумма сил вместо векторной. Как только агент получает травму, клетка, на которой он находится, становится препятствием для всех остальных.Плотность толпы
В реальности толпа не обладает постоянной плотностью. Существуют места, обычно близкие к выходу, где народ располагается очень близко друг к другу, также есть разреженные участки, где между людьми гораздо больше свободного места, такие участки располагаются ближе к хвосту толпы. За плотность толпы отвечает параметр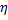 
, так как в модели Кирчнера = 0, если в клетке находится агент, то вероятность на следующем ходе занять эту агента-соседа = 0, так как он получает нулевой выигрыш от любой заполненной клетки. Изменим значения параметра , так чтобы сделать возможным выбор соседней клетки для следующего шага, несмотря на то, что в данный момент она занята.
, так как в модели Кирчнера 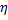= 0, если в клетке находится агент, то вероятность на следующем ходе занять эту агента-соседа = 0, так как он получает нулевой выигрыш от любой заполненной клетки. Изменим значения параметра 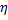, так чтобы сделать возможным выбор соседней клетки для следующего шага, несмотря на то, что в данный момент она занята.
Заметим, что правила, при которых нельзя занимать одну клетку вдвоем не исчезают. Поэтому, если в момент, когда агенты делают шаг, выбранная клетка не освобождается, агент, который ее выбрал, не переходит в нее, а остается на месте.
Если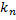 
велико, то толпа плотная, так как агенты выбирают клетки независимо от того, заняты они или нет. Если мало, то агенты предпочитают занимать пустые клетки, что сохраняет просветы в толпе.
велико, то толпа плотная, так как агенты выбирают клетки независимо от того, заняты они или нет. Если 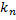мало, то агенты предпочитают занимать пустые клетки, что сохраняет просветы в толпе.Результаты
Модель тестировалась с помощью программного пакета NetLogo 2.0.
Размер модельной сетки – 31 х 31, включая клетки-стены, окружающие сетку.
Результаты на рисунке моделировались для помещения с одним выходом, помещенным в центре стены, никаких других препятствий кроме стен не было (рис.1):
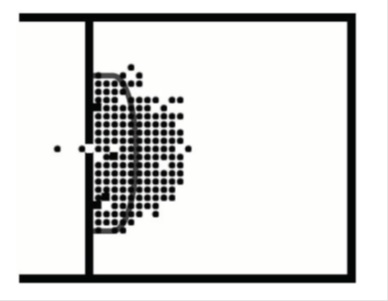
Рис. 1. Модельная сетка
Две сотни игроков были случайным образом размещены по сетке.
Параметры модели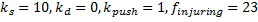 
Чувствительность модели к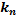 
Посмотрим на количество агентов, оставшихся, в модельной сетке после 350 итераций, в зависимости от 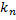(табл.1).
(табл.1).В качестве базовой модели берется модель Кирчнера, где клетка, на которой стоит агент также считается соседней, а параметр 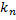не задан.
не задан. = 1 означает очень плотную толпу = 0 означает разреженную толпу
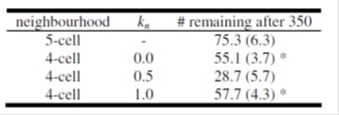
Табл. 1. Чувствительность модели к плотности толпы
Как видно, из таблицы, скорость перемещения к выходу наибольшая (количество агентов, оставшихся в сетке наименьшее) при умеренной плотности толпы.
Преимуществом введения параметра 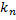является увеличение скорости выхода людей из помещения, так как этот параметр позволяет увеличить частоту выхода до одного за итерацию, тогда как в базовой модели возможен максимум один выход за два прогона модели.
является увеличение скорости выхода людей из помещения, так как этот параметр позволяет увеличить частоту выхода до одного за итерацию, тогда как в базовой модели возможен максимум один выход за два прогона модели.Чувствительность к давлению толпы
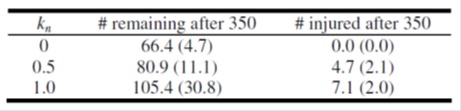
Табл. 2. Чувствительность модели к давлению толпы
При включении в модель предпосылки о давлении толпы, оказываемом на ее участником, становится очевидно, что чем разреженней толпа, тем меньше действуют ее силы на агентов и тем быстрее они добираются к выходу.
Большинство травм в модели наблюдалось в части толпы, близкой к выходу. На рис.1 эта часть отгорожена жирной линией.
Из сравнения таблиц 1 и 2, очевидно, что присутствие давления в толпе на самом деле замедляет время выхода из помещения. Это видно из сравнения количества людей, оставшихся после 350 итераций в помещении в спокойной толпе, и в толпе, применяющей силу.
Другим эффектом, наблюдаемым в толкающейся толпе, является замена регулярных выходов из помещения на череду толчковых выходов и задержек у двери. Такой эффект наблюдается из-за того, что агенты, стоящие по бокам агента, находящегося перед клеткой выхода, толкают его в разные стороны, не давая выйти.
Заключение
В работе представлена агент-ориентированная модель поведения толпы. В отличие от предыдущих работ, посвященных исследованию поведения большого количества людей, в эту модель включена предпосылка о давлении, действующем внутри толпы.
Из-за этого давления толпа может искусственно создавать себе препятствия в виде раненных, тем самым замедляя продвижение к выходу.
Также в модель включается реалистичная предпосылка о том, что агент перемещается на место, на котором стоял другой агент, за один шаг (т.е. одновременно с уходом агента, стоявшего в ячейке). Это позволяет более реалистично моделировать поведение толп.
Оригинал статьи: [«Agent-Based Modelling of Forces in Crowds». Collin M. Henein and Tony White // Multi-Agent and Multi-Agent-Based Simulation Lecture Notes in Computer ScienceVolume 3415, 2005, pp 173-184].