Поведение многих сложных систем, в том числе организаций, сильно зависит от своей сетевой топологии (Albert & Barabási 2002; Barabási 2002; Newman 2003; Watts 2003). Понять эти связи между агентами возможно в том числе при помощи простых симуляционных моделей. В работе были использованы 3 такие модели (рис. 1): первая модель решает задачу о назначениях; вторая модель Курамото представляет организацию в качестве сети осцилляторов; третья модель Лагранжа вносит дополнительные элементы – в частности, он определяет среднюю способность сетевого взаимодействия, которая является предиктором будущей производительности. Все три модели включают в себя абстракции трансфера информации, поведения агентов и общей цели, однако только модель Лагранжа отражает индивидуальные подцели агентов.
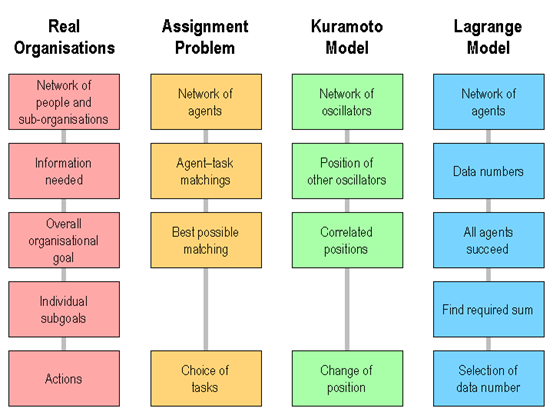
Рис. 1 Сравнение реальных организаций с тремя простыми симуляционными моделями
Метод Кавачи.
В работе используется усовершенствованный метод Кавачи, который случайным образом видоизменяет сетевые структуры без изменения количества связей между агентами (узлами). Эти изменения контролируются при помощи изменения параметра p, имеющего значения [0;5]. Математически, метод Кавачи задает непрерывное отображение множества вероятностных распределений и размерностей (типов) сетей на данном интервале (рис. 2).
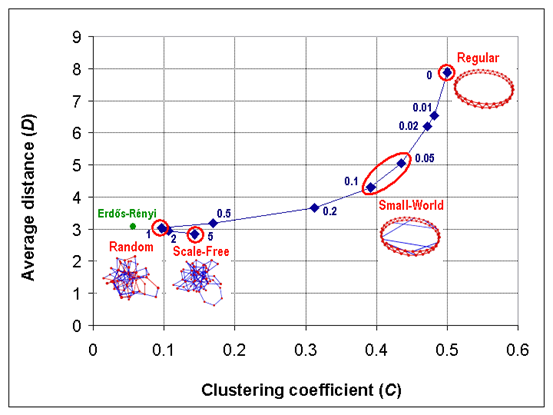
Рис. 2 Графическое представление метода Кавачи
Задача о назначениях.
Первая модель была использована для решения задачи о назначении N агентам N задач, со случайным образом составленной ценовой матрицей C(i, j). Главная задача заключается в нахождении такого соответствия агентов i задачам ti, назначенных таким образом, что каждой задаче будет соответствовать ровно один агент, и для данных назначений минимизируется сумма цен C(i, ti).
Была проведена симуляция с 10000 шагами (итерациями), причем для каждой из 100 случайных ценовых матриц было применено 10 различных топологий, т.е. при помощи метода Кавачи было сгенерировано 1000 случаев.
Качество поведения сети агентов измерялось в процентах при помощи формулы Q=100 C0/C, где C – полные затраты, C0 - минимальные затраты. Это процентное качество варьировалось в промежутке от 9.6% до 32.8%, среднее значение равнялось 18.4%. На основании этих данных было построено уравнение нелинейной регрессии Q=12.5+85.8/D^2, которое объясняет 57% отклонений (корреляция равна 0.76, статистически значима на 10^-100 уровне, рис.3). Поскольку средняя дистанция D между агентами в сети колебалась от 2.6 до 7.9, это уравнение регрессии соответствует среднему качеству выполнения задачи в пределах от 14% до 25%. Экстраполируя данный результат, можно предположить, что если каждый агент был непосредственно связан с любым другим (т.е. D = 1), то качество выполнения будет составлять в среднем около 98%.
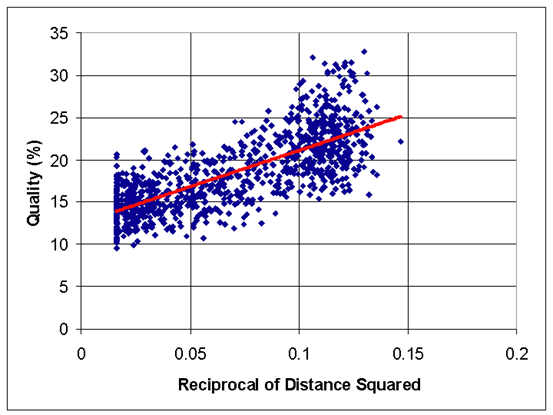
Рис. 3 Результаты симуляции модели задачи о назначениях.
Модель Курамото.
В данной модели агенты в сети принимаются в качестве осцилляторов с частотой колебания fi. Агенты выбирают только позицию или фазу каждого осциллятора (рис. 4), и у них нет другой индивидуальной или общей цели.
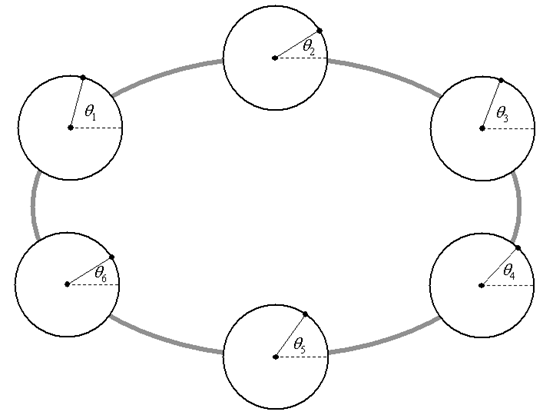
Рис. 4 Шесть осцилляторов Курамото, соединенных в круговую сеть.
Показатель производительности в сети Курамото – корреляция r между фазами всех осцилляторов (Strogatz 2000), которая равна единице, если все осцилляторы синхронизированы:
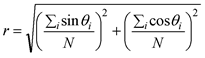
Агенты подталкивают друг друга к синхронизации, двигая среднюю фазу их соседей в сети, причем уровень изменения фазы каждого агента равен:
Было проведено 100000 итераций для выявления самосинхронизации агентов, причем средняя частота fi была низкой (около 0.02).
При помощи метода Кавачи для каждой частоты были сгенерированы по 10 разных сетевых топологий, и эксперимент был проведен 50 раз. Общее число сгенерированных случаев составило 2500.
Синхронизация стала возможна только для низкой ширины частотного распределения (0,001 или меньше), но она достигалась лишь для неупорядоченных и безразмерных сетей (с небольшим средним расстоянием между узлами, рис. 5). Для этих сетей, корреляция r между фазами осцилляторов в среднем равна 0,98.
Теоретический анализ модели Курамото (Kalloniatis 2007) показывает, что способность к синхронизации сохраняется при пропорциональности мультипликатора k и размерности сети к ширине частотного распределения.
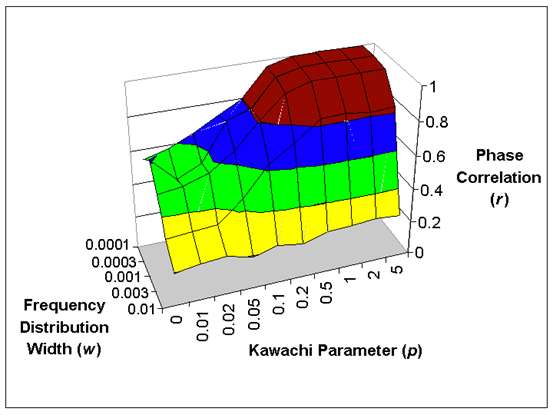
Рис. 5 Средние значения корреляции r между фазами осцилляторов.
При помощи логарифмического преобразования было составлено уравнение регрессии
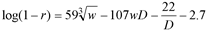 ,
, которое объясняет 74% переменных (корреляция равна 0.86, статистически значима на 10^-100 уровне).
Модель Лагранжа.
В данной модели у каждого агента в сети есть проблема, которая может быть решена в случае получения четырех подходящих «частей решения» от других агентов, что вынуждает их кооперироваться и обмениваться информацией друг с другом.
В данной работе каждому агенту присваивалось значение в интервале [0;59]. Каждый агент должен был найти такие 4 числа, чтобы их сумма соответствовала присвоенному значению из промежутка [33;62], т.е. решала проблему (согласно теореме Лагранжа, такую сумму можно найти всегда). При этом агенты могут только получать номера других агентов, складывать их и сравнивать сумму с требуемым значением для решения проблемы.
При этом, для агента предлагаемые значения являются полезными, если они частично или полностью решают проблему (к примеру, агент, для которого сумма должна составлять 33, и он уже получил значения 25 и 0, значение 4 будет полностью решать проблему (25+0+4+4=33), а значение 1 - частично (25+0+1+1=27)).
На первом шаге агенты сообщают своим «соседям» свое присвоенное число. Далее они предлагают случайно выбранные числа, которое являются для них полезными. Однако, с вероятностью I, соответствующей присвоенной степени иррациональности, агенты начинают ошибаться, то есть предлагать бесполезные или не предлагать полезные значения.
Было сгенерировано 7000 разных случаев (7 степеней иррациональностей, 10 сетевых топологий, повторение 100 раз). В каждом эксперименте было зафиксировано время выполнения задачи T, которое равнялось t в случае успешного выполнения за 1000 шагов, или 1000 (f + 1), f > 0, если проблема оставалась нерешенной за 1000 шагов (рис.6).
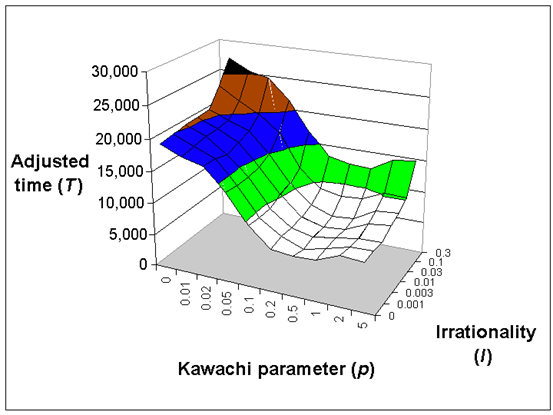
Рис. 6 среднее скорректированное время выполнения задачи T.
Эксперимент был также выполнен для сети типа «футбольный мяч», у которой средняя дистанция D между агентами (узлами) и коэффициент кластеризации равны 3.5 и 0 соответственно. Среднее время выполнения задачи T для данной сети составило 3130 шагов. Ключевая особенность такой сети заключается в том, что агенты, расположенные далеко друг от друга, соединены также через «центр мяча», что дает им возможность обмениваться информацией при помощи K различных путей.
Лучшим предиктором в таком случае является кубический полином T = 22,200*I - 58.9*D^3 - 15,700*K + 2,600*K*D + 30,500, который прогнозирует 76% отклонений (корреляция 0.87, статистически значимо на 10^-30 уровне). На рис. 7 контурные линии отражают значения этого полинома.
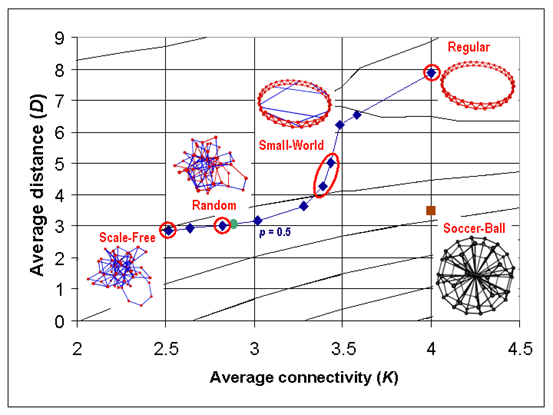
Рис. 7 Изменение средней дистанции D и средняя способность сетевого взаимодействия K.
Результаты.
В первой модели наилучшие результаты достигались в сетях с малой дистанцией D между агентами, особенно в неупорядоченных и безразмерных сетях. Эти данные подтверждают другие исследования, демонстрирующие преимущества неформальных связей с близкорасположенными агентами (Warne et al. 2005).
Вторая модель подтверждает вышесказанное и позволяет изменять иррациональность в поведении агентов. Так, агенты, действующие нерационально, самосинхронизируются или с большим трудом, или вообще не способны этого сделать.
Наконец, третья модель подтверждает предыдущие результаты и добавляет еще один фактор. Так, самая эффективная сетевая топология является средним между неупорядоченной и «малой мировой» (Small-World) сетями благодаря балансу между малой дистанцией D агентами и способностью сетевого взаимодействия на большом расстоянии. В связи с этим было введено понятие средней способности сетевого взаимодействия, определяемое как среднее число независимых сетевых путей между агентами (узлами). Потребность в независимых информационных каналах вызвана тем, что человеческие и организационные ошибки могут блокировать определенные виды информационных потоков. Это является одной из причин, почему неформальные связи дополняют формальные структуры (Warne at al. 2005).
Оригинал статьи: Dekker, Anthony (2007). 'Studying Organisational Topology with Simple Computational Models'. Journal of Artificial Societies and Social Simulation 10(4)6.
