Агент-ориентированная динамическая модель российского фармацевтического рынка

Автор:

Введение

В последнее время в России активно ведётся политика государственного регулирования фармацевтического рынка. С 2010 г. в качестве инструмента политики регулирования используется ограничение максимальных отпускных цен на препараты из устанавливаемого государством перечня жизненно-необходимых и важных лекарственных средств (далее - ЖНВЛС). Оценка эффективности проводимой политики является интересной и актуальной задачей. Для ее решения была разработана агент-ориентированная динамическая модель российского фармацевтического рынка, описание которой будет представлено далее.

Описание модели

Распространенный подход к моделированию влияния экономической политики государства – CGE-моделирование [1-4]. Ориентируясь на данный подход, анализ политики эффективности государственного регулирования фармацевтического рынка может быть осуществлен путём расчёта равновесного состояния после применения новой политики. Согласно модели общего равновесия Вальраса, новое равновесное состояние для всех рынков будет равновесием на каждом из отдельных рынков.

В классической модели Вальраса рынками являются – товарный рынок, рынок капитала и рынок труда. В разработанной нами модели рынками являются различные сегменты фармацевтического рынка. Для выделения сегментов, весь фармацевтический рынок разделён по трём аналитическим разрезам:

1) производитель лекарственного препарата;

2) торговое наименование лекарственного препарата;

3) регион сбыта препарата.

Модификация, представленная в данной работе, состоит в том, что равновесное состояние всего фармацевтического рынка в рассматриваемой модели возникает в случае, когда спрос и предложение уравновешены для каждого сочетания аналитических разрезов.

В качестве базовой модели спроса и предложения в данной работе используется паутинообразная модель равновесия в форме системной динамики [10].

В модели представлены следующие агенты:

1) Обобщенный потребитель фармацевтических препаратов.

2) Производители фармацевтических препаратов. Отдельными агентами являются 10 крупнейших производителей фармацевтических препаратов

3) Государство.

Схема модели представлена на Диаграмме 1.

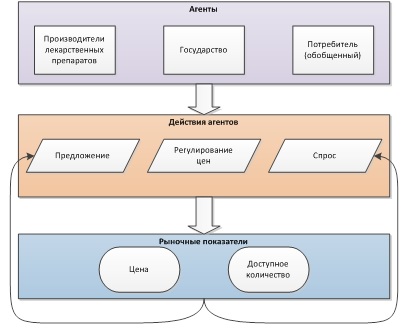
Диаграмма 1. Схема агент-ориентированной модели равновесия фармацевтического рынка

Исходные данные

В качестве информационной базы для анализа и оценки финансового состояния предприятий были использованы результаты аудита продаж лекарственных препаратов в розничном, госпитальном и ДЛО сегменте за 5 лет, а также информация из государственного реестра предельных отпускных цен на лекарственные препараты. В качестве источника данных была использована база данных агентства IMS Health [8].

Алгоритм поведения производителей лекарственных препаратов

Агенты любого типа при формировании своего продуктово-регионального ассортимента используют методологию портфельного анализа «матрица BCG». В соответствии с данным подходом, производители стараются действовать на двух типах рынков – рынках, где они имеют большую относительную долю рынка; и рынках, которые демонстрируют рост прибыли.

Применительно к построенной модели, поведение агентов заключается в следующем:

1) Агент i (любого типа) всех типов перестают производить товар j в регионе k, если:

- товар j попадает в перечень ЖНВЛС и агент теряет контроль над его ценой;

- доля агента в регионе k ниже минимально допустимой;

2) Агенты первого типа сокращают производство товара j в регионе k, если другие агенты уходят с этого рынка.

3) Агенты второго типа, наоборот, увеличивают предложение на тех рынках, откуда уходят другие игроки.

Подробный алгоритм агента при принятии решения об объеме производства товара (i;j;k) представлен ниже (диаграмма 2).

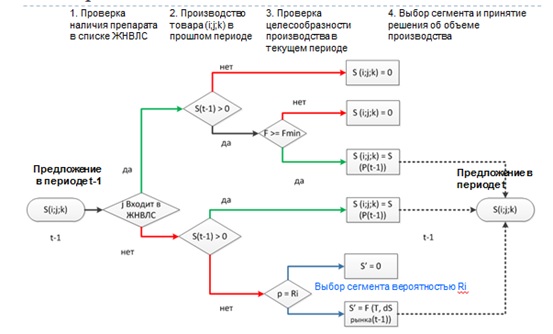
Диаграмма 2. Алгоритм принятия решения об объеме выпуска агентом

Как видно из представленной диаграммы, в каждом периоде времени агент может принять одно из трех возможных решений:

1) Отказ от производства товара (i;j;k).

Агент отказывается от производства в случае, если на товар введено регулирование цен и его доля на рынке товара (i;j;k) меньше минимально приемлемой.

2) Начало производства товара (i;j;k).

Агент может начать производство товара (i;j;k) с вероятностью R_i в случае, если товар (i;j;k) не входит в перечень ЖВНЛС и его производство соответствует стратегии для данного типа агентов T_i.

3) Сохранение производства.

В случае если товар (i;j;k) не входит в перечень ЖВНЛС, а агент в прошлом периоде уже производил данный товар, то его предложение в текущем периоде зависит от уровня цен в предыдущем периоде.

Совокупность принятых агентом за период решений об объеме производства формирует продуктовый портфель агента.

Все агенты в каждый период времени корректируют своё предложение в зависимости от действий других агентов в соответствии со своей стратегией, вероятностью R^I_i и типом агента T^I_i. Если T^I_i= 1, то агент увеличивает предложение лекарственного препарата j в регионе k в пропорции, равной среднему увеличению предложения на рынке в предыдущем периоде.

При T^I_i = -1, агент сокращает предложение в той же пропорции. Данный тип агентов обозначается как агент второго типа.

При T^I_i = 0, предложение агента не зависит от действий других агентов. Данный тип агентов относится к третьему типу.

Далее представлена карта состояний агента на плоскости, формируемой следующим образом:

1. По горизонтальной оси отображается средний уровень цен, предлагаемых агентом.

2. По вертикальной оси отображается количество регионов присутствия агента.

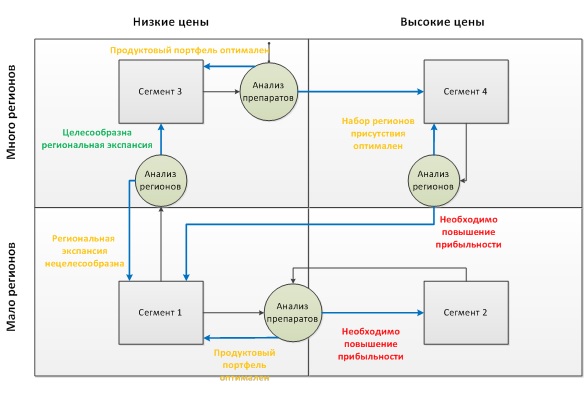
Диаграмма 3. Карта состояний агента

Каждый агент может принимать одно из четырёх возможных состояний, соответствующих сегменту рынка:

1) Сегмент 1. Агенты, продающие лекарства по низкой цене в малом количестве регионов;

2) Сегмент 2. Агенты, продающие лекарства по высокой цене в малом количестве регионов;

3) Сегмент 3. Агенты, продающие лекарства по низкой цене во многих регионах;

4) Сегмент 4. Агенты, продающие лекарства по высокой цене во многих регионах.

Как видно из представленной диаграммы, в зависимости от стратегии агента и рыночных характеристик, в каждый момент времени агенты могут переходить из одного состояния в другое.

Алгоритм вычисления равновесия без государственного регулирования

В качестве основы для построения модели для фармацевтического рынка была выбрана паутинообразная модель, подробно описанная в работе Иезекииля "Теорема Паутины" ("The Cobweb Teorem", 1938) [9].

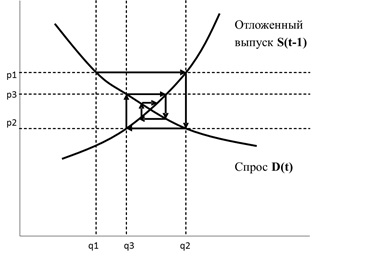
Диаграмма 4. Равновесие в паутинообразной модели

Равновесие вычисляется по следующему алгоритму:

1. В момент времени t в соответствии с функцией спроса определяется ожидаемая равновесная цена P^D , по которой будет приобретено все доступное количество товара.

2. Для препаратов со свободным ценообразованием происходит постепенное изменение цены (в течение времени, определяемого параметром R^PC) до уровня ожидаемой равновесной цены P^D.

3. Новая цена в каждый следующий момент времени формирует новые величины спроса и предложения, которые в свою очередь влияют на доступное количество Q.

Алгоритм вычисления равновесия при наличии государственного регулирования

Для препаратов из перечня ЖНВЛС (и их заменителей) спрос меняется на величину D^'_ijk(t) в соответствии с обратной связью. Если лекарственный препарат входит в перечень ЖВНЛС (j ∈ L), тогда его цена не меняется, а остаётся равной заданной. При этом, когда спрос на данный препарат превышает предложение (которое не меняется из-за фиксированной цены), излишек спроса аллоцируется на другие препараты - D^'_ijk(t), тем самым оказывая влияние на уровень цен препаратов, не входящих в перечень ЖНВЛС.

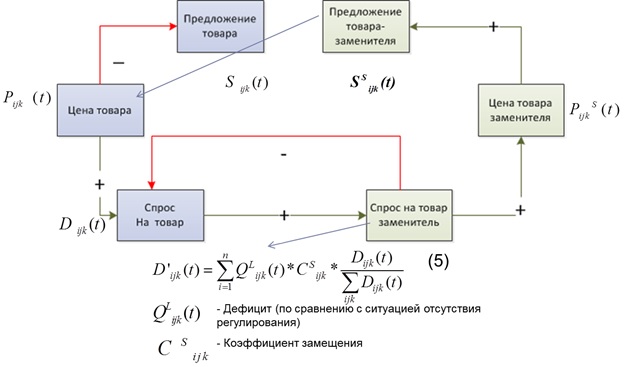
Диаграмма 5. Алгоритм замещения дефицитных лекарственных препаратов

Информационная система «Российский фармацевтический рынок»

Для решения поставленных в работе задач разработанная модель была реализована в системе имитационного моделирования PowerSim. Помимо этого, для автоматизации процесса анализа в систему были добавлены компоненты, позволяющие собирать, компоновать и упорядочивать исходные данные, проводить статистические тесты и представлять результаты в удобном для принятия решения виде.

Ниже приведена общая архитектура построенного решения.

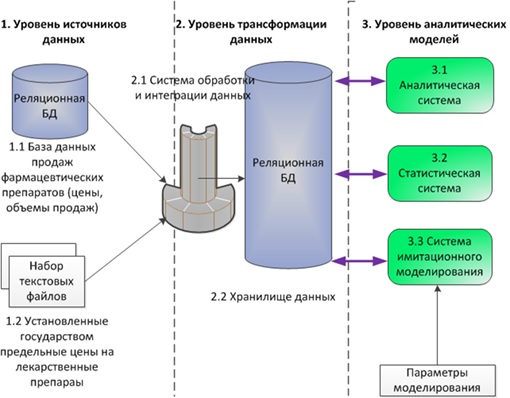
Диаграмма 6. Архитектура аналитической системы на основе динамической модели равновесия фармацевтического рынка

Построенная система включает в себя следующие уровни:

1) Уровень источников данных.

Спецификация динамической модели фармацевтического рынка предполагает ввод в модель существенного объема исходных данных, включая:

• Наборы значений (P_0ijk)– наблюдаемые показатели цены проданных лекарственных препаратов в сегменте. Значения должны быть представлены в виде матрицы P размера I x J x K , где каждый элемент будет являться цена i -го торгового наименования препарата j - го производителя в K -ом регионе.

• Наборы значений (Q_0ijk)– наблюдаемые показатели количества проданных лекарственных препаратов в сегменте. Значения должны быть представлены в виде матрицы P размера I x J x K , где каждый элемент будет являться цена i - го торгового наименования препарата j - го производителя в K-ом регионе.

• Наборы значений (P_rF_ix_ijk)– установленные государством цены i - го торгового наименования препарата j - го производителя в K-ом регионе.

2) Уровень трансформации данных.

Основные функции уровня трансформации данных включают:

• приведение данных из используемых источников к единому формату;

• подготовку данных для их последующей обработки в аналитических приложениях.

3) Уровень аналитических моделей.

В рамках данной работы данные анализируются с помощью трех аналитических приложений

1) Система анализа и представления данных QlikView. Данная система позволяет в режиме реального времени делать запросы к большим объемам данные. В рамках данного исследования, аналитическое приложение позволяет делать прогноз по рынку в целом, а также применять результаты, полученные в других приложениях ко всему массиву данных. С ее помощью также выполнена визуализация результатов моделирования.

2) Система статистического анализа данных IBM SPSS. В рамках данной работы статистический пакет IBM SPSS применяется для построения различных регрессионных моделей и проверки статистических гипотез на длительных периодах наблюдений. В частности, были проведены следующие виды статистического анализа:

1. Выявление факторов, влияющих на цену лекарственных препаратов;

2. Исследование причинно-следственных связей;

3. Тестирование гипотез о наличии сезонных колебаний цен лекарственных препаратов;

4. Тестирование качества прогноза разработанной динамической модели равновесия фармацевтического рынка.

3) Система имитационного моделирования PowerSim. В рамках данного исследования, разработанная агент-ориентированная динамическая модель равновесия фармацевтического рынка была реализована в среде имитационного моделирования PowerSim.

Разработанная модель выглядит следующим образом:

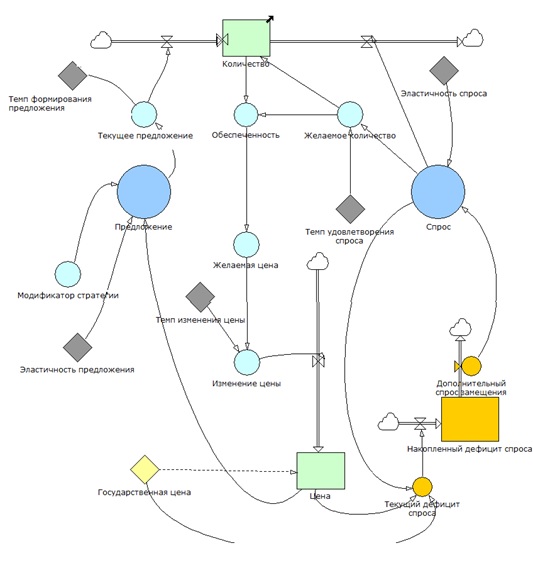
Диаграмма 7. Концептуальная модель Rus_Pharma_Market_Dynamic_Model

Рассмотрим поведение агентов в период с 2013 по 2015 год. Для моделирования динамики поведения агентов использована сегментная матрица следующего вида:

- по оси X определен средний уровень цен производителя;

- по оси Y определено количество регионов присутствия производителя.

В работе проведено сравнение последствий реализации возможных сценариев государственного регулирования фармацевтического рынка:

1) «Мягкий» сценарий – перечень лекарственных препаратов, цены на которые регулируются, включает до 33% от общего числа доступных лекарственных препаратов на рынке.

2) «Жесткий» сценарий – перечень лекарственных препаратов, цены на которые регулируются, включает до 66% от общего числа доступных лекарственных препаратов на рынке.

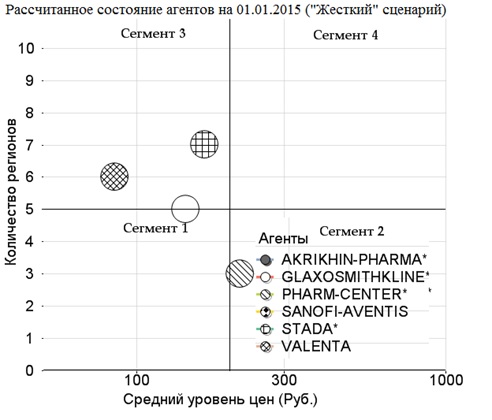
Диаграмма 8. Динамика агентов при "жестком” сценарии регулирования

Анализ показал, что при «жесткий» сценарий приводит к следующим последствиям:

1) «Жесткий» сценарий вынуждает производителей реализовывать продукцию более низких ценовых сегментов.

2) При «жестком сценарии» регулирования часть производителей полностью уходят с российского фармацевтического рынка.

3) При «жестком сценарии» моделирования все агенты сокращают своё присутствие в ряде регионов.

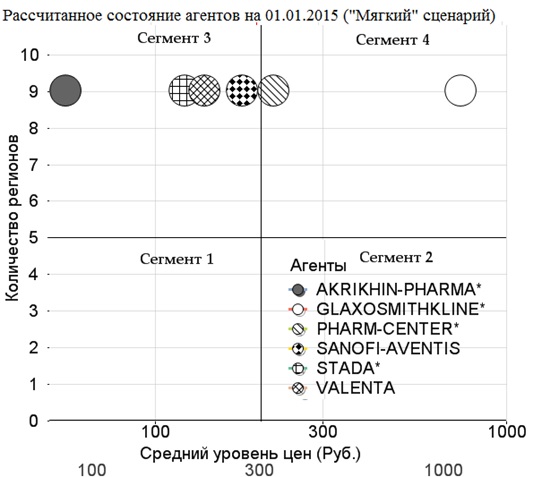
Диаграмма 9. Динамика агентов при "мягком" сценарии регулирования

Согласно проведенным расчётам, при «мягком» сценарии государственного регулирования, последствия существенно отличаются от «жесткого» сценария:

1) Сокращения присутствия агентов в регионах и на рынке в целом не происходит.

2) Некоторые агенты переходят в сегменты с более высокими ценами, остальные агенты сохраняются свой ценовой уровень.

Выводы

С помощью разработанной агент-ориентированной модели равновесия российского фармацевтического рынка были проведены вычислительные эксперименты на реальных данных о продажах фармацевтических препаратов в РФ в период с 2010 по 2012 годы. Проанализировано влияние государственного ценового регулирования на поведение производителей лекарственных препаратов (агентов модели). Результаты анализа показали, что введение государственного регулирования цен на препараты, входящие в перечень ЖНВЛС приводит к следующим негативным последствиям:

1) повышению цен на препараты, не входящие в перечень ЖВНЛС;

2) уходу некоторых ключевых игроков с ряда продуктовых и региональных рынков;

3) стремлению небольших и средних производителей к переходу в сегменты с более высокой ценой.

Литература

1. Johansen, L. (1960). A multisectoral study of economic growth, NorthHolland, Amsterdam.

2. Taylor, L. (1990b). Structuralist CGE models, in L. Taylor (ed.), Socially relevant policy analysis: structuralist computable general equilibrium models for the developing world, MIT press, Cambridge, pp. 1–70.

3. Макаров В.Л., Бахтизин А.Р., Сулакшин С.С. Применение вычислимых моделей в государственном управлении / Научный эксперт, 2007.

4. Макаров В.Л., Бахтизин А.Р. Эффективный способ оценки государственной политики// Экономика и управление, Уфа, 2001(4).

5. Axelrod R. «The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration», Princeton: Princeton University Press, 1997.

6. Бахтизин А.Р. Агент-ориентированные модели экономики. М.: Экономика, 2008.

7. Форрестер Дж. Основы кибернетики предприятия (индустриальная динамика) / пер. с англ., общая редакция Д. М. Гвишиани. М: Прогресс, 1971.

8. Лычкина Н.Н. Имитационное моделирование экономических процессов. Москва, 2012.

9. Ezekiel, Mordecai (1938), "The Cobweb Theorem," Quarterly Journal of Economics, 52, 255-280. 10. Skraba A. Cobweb Model in System Dynamics Form. System Dynamics Conference, 2006

Назад к списку Следующий